• 面对纷繁复杂的直流电路，许多人一筹莫展，无从下手，今天交给你一招，保你轻轻松松的战胜一切电路问题，那就是三大

• 三大定律：欧姆定律、克希荷夫电流定律、克希荷夫电压定律

• 五大方法：支路电流法、叠加原理、戴维南定理、诺顿定理、节点电压法。

• 下面对此进行详细解释

• 第一个重要定律：欧姆定律:我们在初中刚接触电工学的时候，首先就要学到这个著名的定律了，它反映的是某段导体（电阻）与通过它的电流及两端电压的关系R=U/I。对于全电路来说，是与它关联的另一个公式就是全电路欧姆定律，它将电源的内阻也加进去了，这个比较简单，记住一点，它们是计算某个线性电阻、某段支路的重要定律。欧姆定律是对支路电压、电流、电阻的一种约束。

图一 欧姆定律

• 克希荷夫定律，有的人叫基尔霍夫定律，这个都可以，不要细究，音译过来的。

• 第二个重要定律：克希荷夫电流定律（KCL），又称克希荷夫第一定律：任一瞬间，流入节点的电流的代数和恒等于流出该节点的电流的代数和；广义节点：不是一个节点，可以是一个电路。用该定律可以判断两个电路之间的电流关系。比如两个电路间只有一条导线，则这条导线内电流为零。

• 需要注意的是在计算电路列方程的时候，若是流入节点的（+号）、流出的电流（-）均在式子的一侧，则电流代数和为零，若在式子的两侧，则流入的等于流出的，不加+、-号。如下图I1+I2=I3+I4，或者I1+I2-I3-I4=0.三极管三个电极的电流关系：Ie=Ic+Ib。

• 这个定律是对节点电流的一种约束。

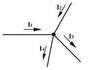
节点电流

• 第三个重要定律：克希荷夫电压定律（KVL），又称克希荷夫第二定律，任一瞬间，在电路内任一闭合回路内的电位升之和，恒等于电位降之和。

• 应用程序：首先画出电阻、电源的正方向；其次选定一个回路；第三，选择顺时针或逆时针方向作为参考方向；第四，按照参考方向，按照电压升为正、降为负的规则依次相加，整个回路的电压和为零。

• 注意电动势方向，是由低电位端指向高电位端，同样受此规则约束，也即电位升为+，电位降为-，不管电压、电动势实际数值如何，均是按照其正方向与环绕方向的关系列式计算的，在其前面加+-号，不受其实际符号的影响，如-Uab=-（-2v）=2v；并且要注意若是升降相加减在等式左边则结果为零，若是升降分别在在等式两边，则应注意方向，否则会计算错误的。

• 克希荷夫电压定律是对回路电压的一种约束。

• 如下图，对于回路acdf,

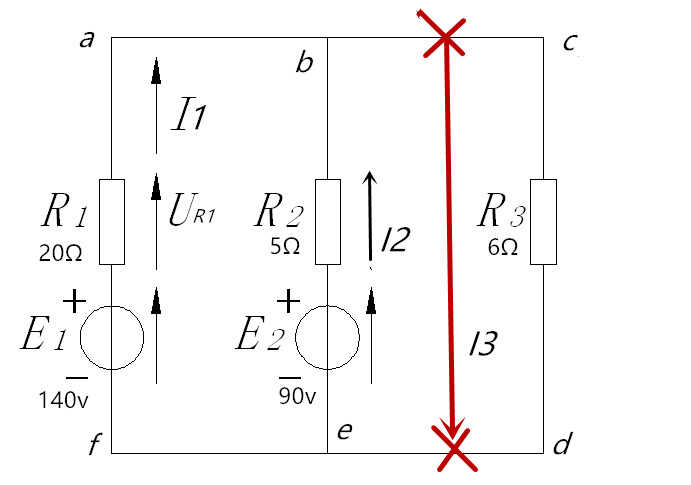
• E1-UR1-UR3=0,对于回路abef，E1-UR1+UR2-E2=0,对于回路bcde，E2-UR2-UR3=0

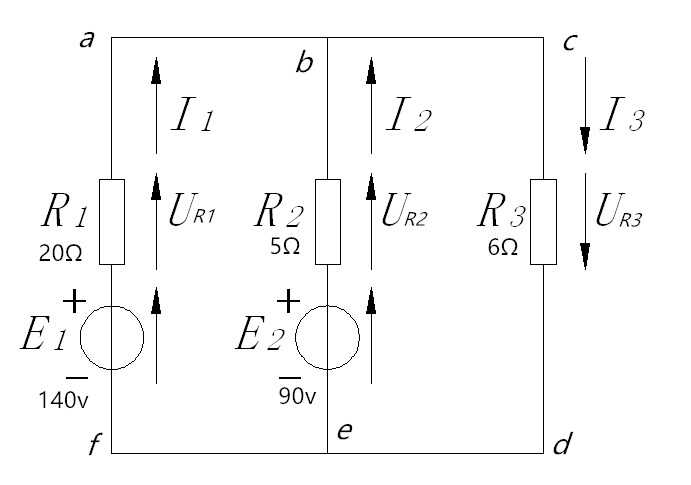
图二 直流电路计算图

• 以上三个定律具有普遍性，适用于由各种不同元件组成的电路，也适用于任何变化的电流和电压。

• 五大方法

• 第一个方法：支路电流法。支路电流法 应用克希荷夫电流、电压定律列方程求各支路电流的方法。

• 设电路又b条支路，有n个节点，则根据克希荷夫第一定律可得出n-1个独立方程；根据克希荷夫第二定律可得出b-（n-1）个独立方程；利用两个定律可得出（n-1）+[b-（n-1）]=b，也即有几条支路，就可以列几个独立方程。

• 如上图二所示，可以列出以下三个方程组1、2、3，分别是利用的是KCL、KVL定律，求出了各支路的电流。

• 第二个方法·.叠加原理。对于线性电路，任何一条支路中的电流，都可以看成是由电路中各个电源（电压源或电流源）分别作用时，在此支路中所产生的电流的代数和。但功率的计算就不能用叠加原理。从数学上看，叠加原理就是线性方程的可加性，其不仅可以用来计算复杂电路，而且也是分析与计算线性问题的普遍原理。

• 电路单独作用，就是假设将其余电源均除去（将各个理想电压源短接，即其电动势为零，将各个理想电流源开路，即其电流为零，但它们的内阻应该保留在电路中）

• 这个从原理上来说比较好理解，但在应用中比较复杂，计算也容易出错，一般很少使用，列在这里是作为一种对线性电路的理解。

• 第三个方法：戴维南定律。凡是具有两个输出端的部分电路，称为二端网络，有电源的称为有源二端网络，可以简化成一个等效电源，可用一个具有电动势为E与内电阻为r0相串联的等效电压源代替。无电源的称为无源二端网络，可用一个等效电阻代替。

• 任何一个线性有源二端网络，就其对外电路而言，都可用一个具有电动势Ｅ和内电阻r0的等效电压源来代替。Ｅ为该有源二端网络的开路电压，r0为该网络中，电源除去以后，无源二端网络的等效电阻（电压源短路，电流源开路）。戴维南定理又称为等效电源定理。可以很方便的求解某支路的电流。

• 如上图二，利用戴维南定理求各支路电流，可以先求出I3，将R3支路取出，如下图所示，从红线处断开，求开路电压U，这样一来电路就简单了，E1E2R1R2为串联关系，可以很简便的求出电流I

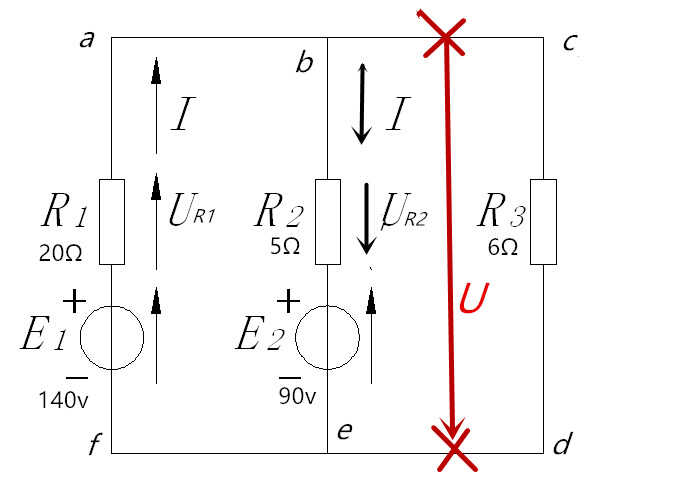
戴维南定理第一步

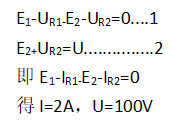
求的开路电压

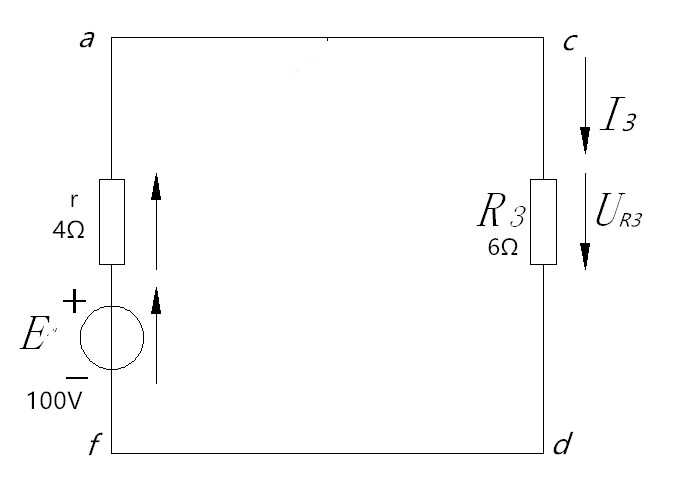
• 将E1E2短路后，电阻R1R2为并联关系，求的内阻r=4Ω，将支路R3串入电压源电路，如下，电路非常简单了，可求的I3=10A，和上面支路电流法求的的结果是一样的。然后依次求其它支路即可。

• 通过以上计算，我们总结出利用戴维南定理解决电路问题的步骤：

• A.将待求支路从电路中提出；

• B.把待求支路断开，求有源二端网络的开路电压E0；注意，这时的计算同正常计算一样，原有的电路中的电源、电阻均不动，但应注意电流方向应该根据实际电路而改变。

• C.求无源二端网络的等效内电阻r0；注意这时应该将电压源短路、电流源断路，而电阻的连接方式不变。

• D.把待求支路接入由E0和r0组成的等效电压源电路，用全电路欧姆定律求解。

• 第四个方法：诺顿定理任何一个有源二端线性网络均可以用一个电流为Is的理想电流源和内阻R0相并联的电源来代替。等效电源的电流就是有源二端网络的短路电流，即将a、b端（待求支路）短接后其中的电流。等效电源的内阻等于有源二端网络中所有电源除去（电压源短路、电流源开路）后所得到的无源网络a、b两端之间的等效电阻。这就是诺顿定律。

• 将待求支路R3取出，求短路电流I3,I3=I1+I2=7+18=25A，内阻同上r=4Ω；

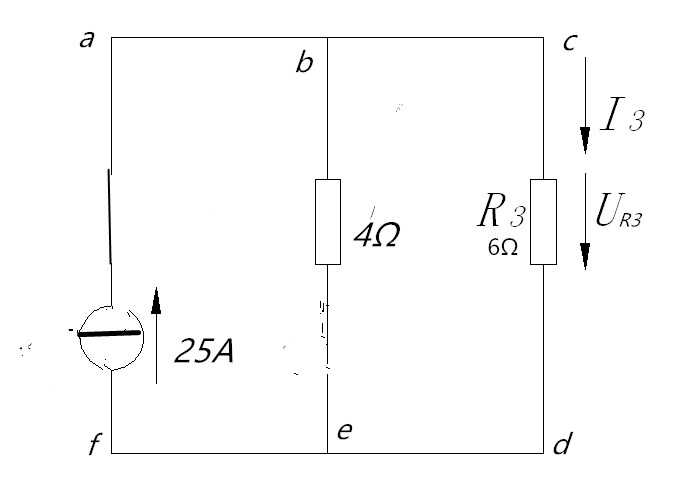
等效电流源

• 内阻r与R3为并联关系，可以很轻松的求出I3=10A，和上面的计算结果是一样的。

• 通过以上计算我们可知利用诺顿定理解决问题的步骤

• A.将待求支路短接，求短路电流，同一般计算方法一样；

• B.求等效内电阻r0；注意不能将待求支路短路，而是断路后求二端网络电阻；

• C.将待求支路并入等效电阻r0，求解。

• 第五个方法：节点电压法。只有两个节点a和b的情况下，节点间的电压U称为节点电压。若知道电动势和电阻的情况下，只要先求出节点电压，就可以计算各条支路电流了。

• 节点电压公式。节点电压等于各条支路的电动势与电阻的商之和与各条支路电阻倒数之和的比，对于分母指的是所有电阻，包含没有电动势的支路。 在上式中，分母的各项总为正，分子的各项可以为正，也可以为负。当电动势和节点电压的正方向相反时取正号(简称为反正），相同相同时取负号。注意分子、分母均是除数关系。

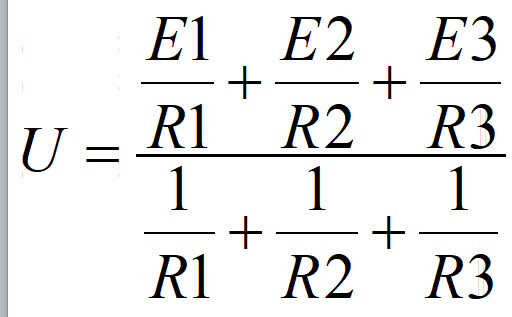
• 上面的例子就是非常典型的两个节点

• 可求的

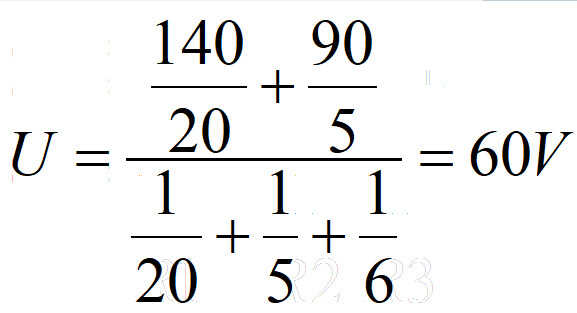
• 则I3=60/6=10A，和上面的计算结果是一样的。

• 我们在实践中可以灵活应用上述方法，根据不同的电路形式，选择不同的解决方法，这样可以很快的得到结果。