一、一般的串并联，这个不用说了，大家都会

二、结点法

即将每个节点都标上一个电势（标上电势指的是：先选一个结点作为零电势，根据电压就是电势差标出其他电势，同一根导线连接的两点的电势相同，如果两个点的电势相同，那么可以拆掉这两个节点之间的电阻）然后画一张新的图，将所有不同的电势按顺序排列，将所有电阻画在连着相同电势的节点的第二张图中再算

三、对称法

如果一个图关于一条对称轴对称（即对应结点和电阻阻值都相同）把图像沿对称轴翻折得到新的图，等效电阻为原来所处位置的电阻的一半。

四、无穷法：

1.方法一：先设电阻为x，然后取一段相同的东西一样是x，列出方程求出x

2.方法二：也可以先算n（n为自然数）个东西拼在一起的电阻是多少，然后取极限，和数列递推差不多。这个方法的优点是可以算出有限个的值，缺点是对数学要求比较高。

五、用基尔霍夫定律求电阻：

1.基尔霍夫定律：

（1）电流定律：

所有进入某节点的电流的总和等于所有离开这节点的电流的总和。

或者描述为：假设进入某节点的电流为正值，离开这节点的电流为负值，则所有涉及这节点的电流的代数和等于零。

（2）电压定律：

沿着闭合回路所有元件两端的电势差（电压）的代数和等于零。

或者描述为：沿着闭合回路的所有电动势的代数和等于所有电压降的代数和。

2.利用基尔霍夫定律求电阻：

（1）第一步：比如说我们要求的是AB之间的电阻，那么给AB一个电压U等效于在AB之间加一个电压为U的电池。（请注意，通过电池是有电流的，电池两端是有电势差的，计算节点的电流和闭合回路的时候千万不要漏掉），然后将所有通过两点之间的电流全部设出来，根据电压等于电流乘以电阻设出电压，然后用一大堆基尔霍夫定律列出方程，这是一个一次方程组，所以解起来不会很难。

当基尔霍夫定律用得熟练之后就不需要列很多方程了，因为有些东西一眼就能看出来，比如说有一个节点有联通三个其他节点，其中两个流入i和j，那么另一个一定流出i+j

（2）求出电阻，R*=U/I*，I*为通过电池的电流。

六、星角变换（△-Y变换）：

1.三端电阻网络

任何一个三段纯电阻网络都可以等效为以下两个电路：

 

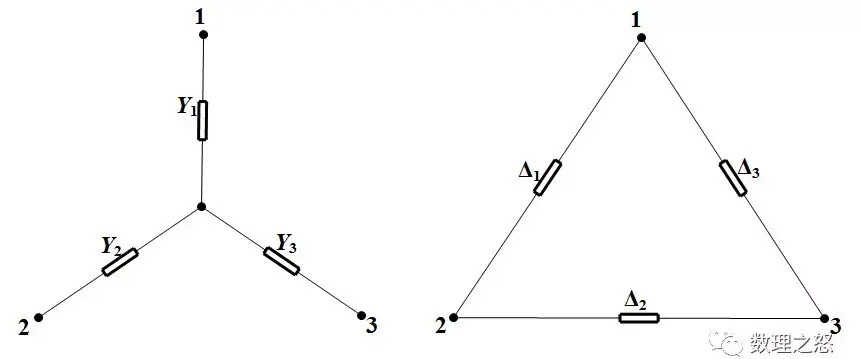
我们把左边的电路叫做星形电路，右边的电路叫做三角形电路。

2.星角变换

星角变换指的是星形电路和三角形电路之间的互换，它的公式如下（以上图的字母）

 

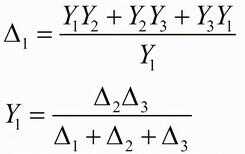
七、叠加原理：

1.多个电池的合作用效果等于它们分别作用的效果之和

这句话是什么意思呢？比如说我们有一个电阻R，规定电流方向向右为正，假设只有电池k（此时其余电池看做导线），通过R的电流为I_k，则所有电池一起作用时，通过R的电流为∑i_k。

2.戴维宁（南）定理

任何一个二端电阻网络（只有电池和电阻，且电池和电阻可以任意多个）都可以看做一个无内阻电池和一个电阻串联（或者看做一个有内阻的电池）