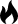图片1半球与圆柱孔相贯示意图

1.半球与圆柱孔相贯的情况

当一个半球体与一个圆柱孔相贯时，会出现三种情况

（1）圆柱孔穿过半球体的底面。

（2）圆柱孔与半球体的底面相切。

（3）圆柱孔完全包含在半球体内部。

2.解决方法

解决半球与圆柱孔相贯问题，需要用到以下几个几何学知识

（1）平行关系两个平面或两条直线在同一平面内，且它们不相交，则称它们平行。

（2）相交关系两个平面或两条直线在同一平面内相交，称它们相交。

（3）相切关系两个圆或球在同一平面内，恰好只有一个交点，则称它们相切。

（4）相似关系两个图形的形状相同，但大小不同，则称它们相似。

（5）投影关系在同一平面上，从一个点向某个方向发出的线段，在另一个点上的投影点相同，则称这两个点在同一直线上。

3.解决步骤

根据上述几何学知识，解决半球与圆柱孔相贯问题的步骤如下

（1）确定圆柱孔的位置和大小。

（2）在半球体上作圆形投影，确定圆柱孔在半球体上的位置和大小。

（3）根据圆柱孔在半球体上的位置和大小，将半球体分成不同的部分。

（4）对每个部分，根据相似关系，计算出它们的体积。

（5）将所有部分的体积加起来，即可得到半球与圆柱孔相贯的体积。

图片2半球与圆柱孔相贯示意图

本文通过详细的图片解释，让读者了解了半球与圆柱孔相贯问题的解法。通过掌握这个问题的解法，读者可以更好地理解几何学知识，提高自己的数学水平。

本文主要介绍半球与圆柱孔相贯的几何学问题，通过图片详细展示相贯的情况和解决方法，帮助读者掌握这一几何学技能。

什么是半球与圆柱孔相贯？

半球与圆柱孔相贯是指一个半球体与一个圆柱体的孔相交的情况。如下图所示，半球体和圆柱体的孔相交。

如何计算半球与圆柱孔相贯的面积？

首先，需要计算出圆柱体的侧面积和半球体的表面积。然后，根据相交部分的形状计算出相交部分的面积。，将圆柱体的侧面积、半球体的表面积和相交部分的面积相加即可得到半球与圆柱孔相贯的面积。

例如，下图所示的半球与圆柱孔相贯的面积计算公式为

其中，S1为圆柱体的侧面积，S2为半球体的表面积，S3为相交部分的面积。通过计算可得，该半球与圆柱孔相贯的面积为

S = S1 + S2 + S3 = πrL + 2πr^2 + πr^2/2 = πr(L + 2r/3)

如何绘制半球与圆柱孔相贯的图形？

通过以下步骤可以绘制半球与圆柱孔相贯的图形

1. 绘制圆柱体的侧面和底面，标注圆柱体的高度和半径。

2. 在圆柱体的侧面上绘制一个圆形，标注圆形的半径和圆心坐标。

3. 在圆柱体的底面上绘制一个圆形，标注圆形的半径和圆心坐标。

4. 绘制半球体的表面，标注半球体的半径和圆心坐标。

5. 根据相交部分的形状，在图形中标注相交部分的形状和大小。

例如，下图所示的半球与圆柱孔相贯的图形

半球与圆柱孔相贯有哪些应用？

半球与圆柱孔相贯在工程学和建筑学中有广泛的应用。例如，在建筑设计中，半球与圆柱孔相贯的形状常常被用作建筑物的装饰元素，如下图所示

此外，半球与圆柱孔相贯还可以用于制造金属、陶瓷等材料的零件，以及制造汽车、飞机等交通工具的部件等。